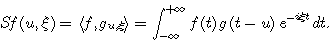
The windowed Fourier transform replaces the Fourier transform's sinusoidal wave by the product of a sinusoid and a window which is localized in time.
It takes two arguments: time and frequency.
The windowed Fourier transform is defined by
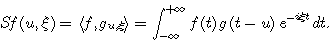
It uses an atom which is the product of a sinusoidal wave with a finite energy symmetric window g. The windowed Fourier transform family of atoms is obtained by time translations and frequency modulations of the original window:
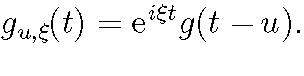
This atom has a frequency center x and is symmetric with respect to u.
The time and frequency spreads of these functions are constant. The family is generated by time and frequency translations of one atom. Here are examples of Heisenberg boxes of windowed Fourier atoms:
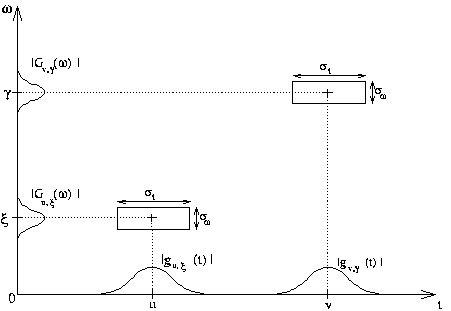
The windowed Fourier transform has a constant time frequency resolution. This resolution can be can be changed by rescaling the window g. It is a complete, stable, redundant representation of the signal. Hence it is invertible. The redundancy implies the existence of a reproducing kernel.
The square modulus of the windowed Fourier transform is the spectrogram of a signal:
The properties of the windowed Fourier transform are determined by the window g, or rather its Fourier transform, whose energy should be concentrated around 0. This energy spread is measured by three parameters.
The Fast Windowed Fourier Transform is equivalent to a sequence of FFTs.