These few examples are made of analytic signals whose intanteous frequencies are known.
They illustrate the windowed Fourier transform's ability to localize instaneous frequencies.
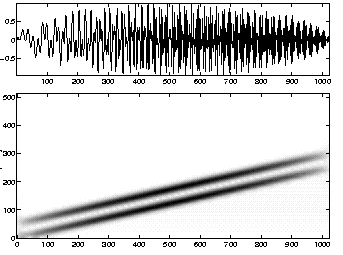
Here is the sum of two parallel linear chirps with its spectrogram.

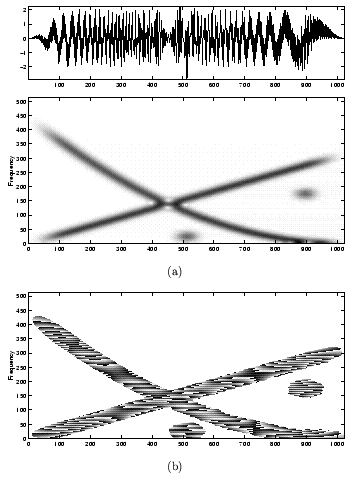
Now a synthetic signal which is the sum of a linear chirp with an increasing frequency, a quadratic chirp with a decreasing frequency, and two modulated gaussians. Below is its spectrogram and the complex phase of its windowed Fourier transform, computed with a gaussian window.
The components of this synthetic signal have explicit instantaneous frequencies.
Here is the sum of two hyperbolic chirps and its spectrogram.
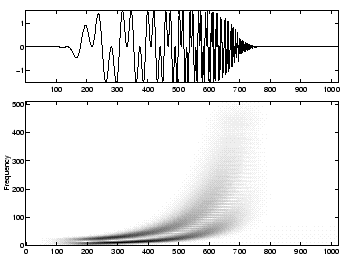
The "instantaneous frequencies" are well tracked in the first example. On the contrary, the spectrogram loses the frequency of the hyperbolic chirp when it becomes high too fast. This is due to the fixed time resolution of the windowed Fourier transform.
In these three examples, it seems that the instantaneous frequencies is traced by the spectrogram's mawima, provided these frequencies are not too close.