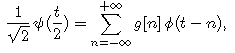
Properties of biorthogonal wavelets are to be compared to the orthogonal case.
As in the orthogonal case, y(t) and j(t/2) are related by a scaling equation which is a consequence of the inclusions of the resolution spaces from coarse to fine:
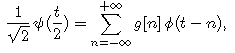
Similar equations exist for the dual functions which determine the filters h2 and g2.
A biorthogonal wavelet has m vanishing moments if and only if its dual scaling function generates polynomials up to degree m. This can be verified by looking at the biorthogonal decomposition formulas.
Hence there is an equivalence theorem between vanishing moments and the number of zeroes of the filter's transfer, provided that duality has to be taken into account. Thus the following three properties are equivalent:
and the dual result is also valid. Duality appears naturally, because the filters determine the degree of the polynomials which can be generated by the scaling function, and this degree is equal to the number of vanishing moments of the dual wavelet.
If the filters h et h2 have a finite support, then the scaling functions have the same support, and the wavelets are compactly supported. If the supports of the scaling functions are respectively [N1,N2] and [M1,M2], then the corresponding wavelets have support [(N1-M2+1)/2,(N2-M1+1)/2] and [(M1-N2+1)/2,(M2-N1+1)] respectively.
The atoms are thus compactly supported if and only if the filters h et h2 are.
Tchamitchian's theorem provides again a sufficient regularity condition. Remember that this condition bears on the filter h which determines the scaling equation. Hence the regularity of the primal atoms are related to the primal filters.
Consider the following decomposition of f:
The number of vanishing moments of a wavelet is determined by its dual filter. It corresponds to the approximating power of the dual multiresolution sequence. This is why it is preferred to synthesize a decomposition filter h with many vanishing moments, and possibly with a small support.
On the other hand, this same filter h determines the regularity of j, and hence of y. This regularity increases with the number of vanishing moments, that is, with the number of zeroes of h.
Unlike the orthogonal case, it is possible to synthesize biorthogonal wavelets and scaling functions which are symmetric or antisymmetric and compactly supported. This makes it possible to use the folding technique to build wavelets on an interval.
If the filters h and h2 have and odd length and are symmetric with respect to 0, then the scaling functions have an even length and are symmetric, and the wavelets are also symmetric. If the filters have an even length and are symmetric with respect to n=1/2, then the scaling functions are symmetric with respect to n=1/2, while the wavelets are antisymmetric.
Spline wavelets and scaling functions are an interesting example of biorthogonal systems. One of the scaling functions is a B-spline. A coefficient table is available. There is a general closed form formula for these filters.