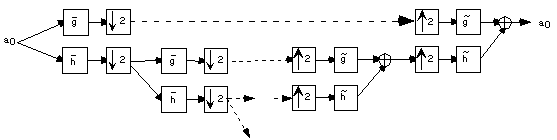
Les ondelettes et fonctions d'échelles biorthogonales sont caractérisées par un banc de filtres à reconstruction parfaite; les ondelettes et fonctions d'échelles orthogonales sont caractérisées par une paire de filtres miroirs conjugués. Néanmoins, tout banc de filtres à reconstruction parfaite (ou filtres miroirs conjugués) ne correspond pas à un système d'ondelettes. En effet, il faut prendre garde à la stabilité des schémas de décomposition et de reconstruction lorsque le nombre d'échelles augmente, cette à dire lorsqu'on met en cascade une infinité de bancs de filtres. Cela se traduit par la condition supplémentaire (7.37) sur le filtre miroir conjugué h pour qu'il définisse une fonction d'échelle.
On peut de même effectuer la décomposition du signal a1 en un signal a2 et un signal d2; en répétant cette opération on crée un signal à basse résolution aj et une suite de signaux de détails d1 .... dj.
On peut faire une décomposition récursive analogue en utilisant l'algorithme à trous et engendrer ainsi un signal à basse résolution Aj et une suite de signaux de détails D1 .... Dj. Les deux décomposions sont liées par la relation suivante:
Dans le domaine fréquentiel, le transfert de a0 à Aj vaut
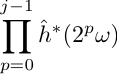
Effectuons un changement d'échelle T = 2-jt de sorte que l'intervalle entre les échantillons non nuls du filtre le plus large soit 1 quelque soit j. Alors l'intervalle entre les coefficients non nuls du filtre le plus étroit est 2-j. Le transfert devient
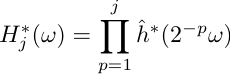
Faisons tendre j vers l'infini. Si le transfert
ci-dessus converge dans L2, on peut l'interpréter la limite comme la transformée de Fourier du miroir d'une fonction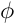 
et la transformation du signal de départ s'écrit
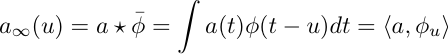
qu'on interprète comme le produit scalaire avec le translaté de la fonction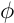 
dont la transformée de Fourier est
La fonction 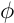satisfait nécessairement une équation
d'échelle:
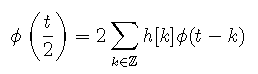
De telles fonctions sont au cœur des analyses multirésolutions, qui sont elles-mêmes à la base des ondelettes dyadiques.