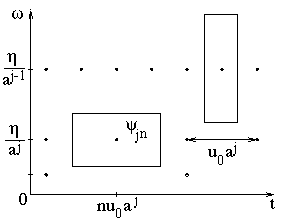
Pour recouvrir le plan temps-fréquences avec des boîtes de Heisenberg d'ondelettes, on n'utilise pas une grille à pas fixe, mais avec des pas de temps inversement proportionnel à l'intervalle fréquentiel, lui-même proportionnel à l'échelle.

On suppose que l'ondelette satisfait à la condition de reconstruction
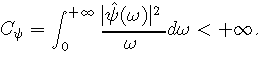
qui garantit l'inversibilité de la transformée en ondelettes. Daubechies donne des conditions nécessaires à l'obtention d'une frame à partir du pavage ci-dessus:
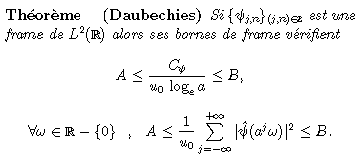
Il existe aussi des conditions suffisantes.
Par comparaison aux frames de Fourier fenêtrées, on note que
Dans les deux cas (Fourier ou ondelettes), la représentation du signal présente l'inconvénient de ne pas être invariante par translation en temps ou en espace. Or les structures qu'on cherche souvent à mettre en évidence ne sont pas naturellement réglés sur des intervalles correspondant à ceux des frames. En particulier, la structure du signal peut être dégradée dans les basses résolutions..
C'est pourquoi on s'intéresse aux transformées en ondelettes dyadiques, qui sont discrètes en échelle mais continues en temps (en pratique, cela revient à ne pas sous-échantillonner les signaux quand on passe aux échelles grossières).
Une autre représentation qui commute avec les translation des structures est la représentation par maxima de la transformée en ondelettes dyadique. Elle est moins redondante mais n'est pas complète.
En pratique, l'implémentation de la transformée en ondelettes dyadique utilise des bancs de filtres à reconstruction parfaite qui correspondent à des ondelettes définies à partir d'approximations multirésolutions. Ces bancs de filtres sont particulièrement rapides à calculer.